Repeated measures ANOVA in Python

April 2018

Welcome to this first tutorial on the Pingouin statistical package. In this tutorial, you will learn how to compute a two-way mixed design analysis of variance (ANOVA) using the Pingouin statistical package. This tutorial is mainly geared for beginner, and more advanced users can check the official Pingouin API.

Installation

To install Pingouin, you need to have Python 3 installed on your computer. If you are using a Mac or Windows, I strongly recommand installing Python via the Anaconda distribution.

To install pingouin, just open a terminal and type the following lines:

pip install --upgrade pingouin

Once Pingouin is installed, you can simply load it in a python script, ipython console, or Jupyter notebook: 

import pingouin as pg

Simulate the data

For the sake of the example, let's say that we are interested in how meditation can improve school performances in primary school students. If we want to study that, one way would be to split a group of student into a control group and a meditation group, i.e. a certain number of students will be instructed to meditate for 20 minutes a day every day of the week, while the remaining students will be instructed not to change anything to their usual daily routine. This factor is our between-group factor.

Now, we want to examine how meditation significantly improves or worsens the performances over time, starting from the beginning of the school year (August) to the end of the school year. To study that, we are going to asses their school performances at three time points during the year: August (or time = 0 months), January (time = +6months) and June (time = +12 months).

To sum up, we have:

  • A dependent variable: the test scores
  • A within-group variable, time of the year, with three levels (August, January, June)
  • A between-group variable, Group, with two levels (Control, Meditation)
  • A subject variable, Subject
Let's generate this fake dataset using Numpy and Pandas: 

import pandas as pd
import numpy as np

# Let's assume that we have a balanced design with 30 students in each group
n = 30
months = ['August', 'January', 'June']

# Generate random data
np.random.seed(1234)
control = np.random.normal(5.5, size=len(months) * n)
meditation = np.r_[ np.random.normal(5.4, size=n),
                    np.random.normal(5.8, size=n),
                    np.random.normal(6.4, size=n) ]

# Create a dataframe
df = pd.DataFrame({'Scores': np.r_[control, meditation],
                   'Time': np.r_[np.repeat(months, n), np.repeat(months, n)],
                   'Group': np.repeat(['Control', 'Meditation'], len(months) * n),
                   'Subject': np.r_[np.tile(np.arange(n), 3),
                                    np.tile(np.arange(n, n + n), 3)]})

We can print the first lines of our dataframe using df.head():

DATAFRAME
Group Scores Time Subject
Control 5.9714 August 0
Control 4.3090 August 1
Control 6.9327 August 2
Control 5.1873 August 3
Control 4.7794 August 4

Descriptive statistics

Now let's take a look at our data using the Seaborn package:

import seaborn as sns
sns.set()
sns.pointplot(data=df, x='Time', y='Scores', hue='Group', dodge=True, markers=['o', 's'],
	      capsize=.1, errwidth=1, palette='colorblind')

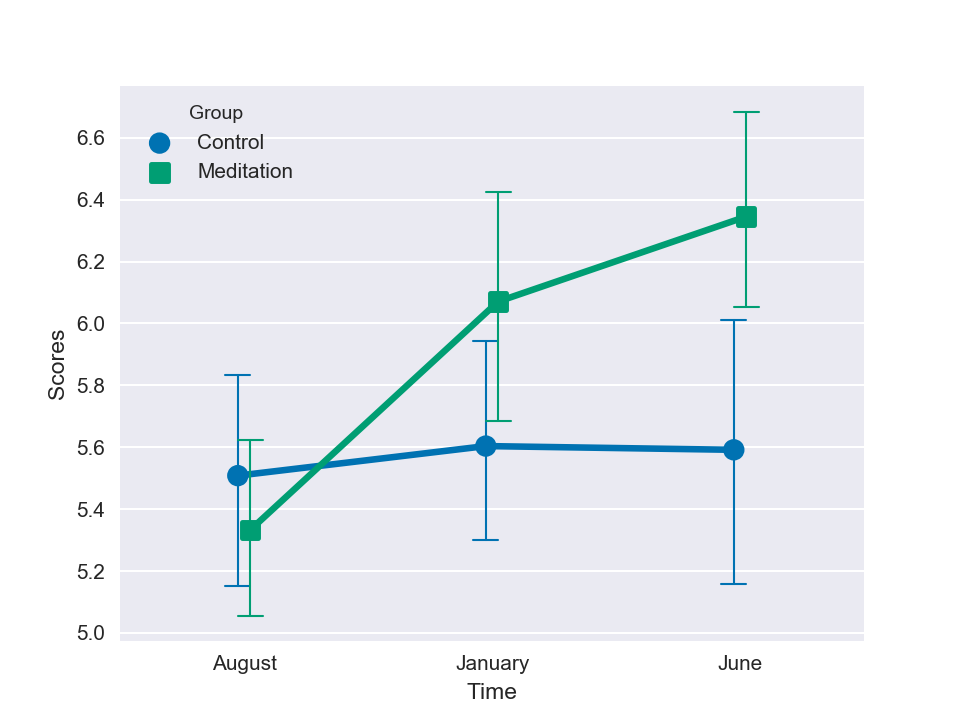
Visually, we can already see a clear improvement of the test scores over time in the meditators group. Let's look at the mean and standard deviations of the data:

df.groupby(['Time', 'Group'])['Scores'].agg(['mean', 'std']).round(2)

MEAN AND STD
Time Group Mean STD
August Control 5.51 1.03
August Meditation 5.33 0.81
January Control 5.60 0.90
January Meditation 5.97 1.07
June Control 5.59 1.18
June Meditation 6.35 0.93

ANOVA

To test the significance of this effect, we will need to use a mixed-design ANOVA. That is where Pingouin comes into play. We are going to use the mixed_anova function with the following input arguments:

  • dv: name of the column containing the dependant variables
  • within: name of the column containing the within-group factor.
  • between: name of the column containing the between-group factor.
  • data: name of the pandas dataframe
import pingouin as pg
# Compute the two-way mixed-design ANOVA
aov = pg.mixed_anova(dv='Scores', within='Time', between='Group', subject='Subject', data=df)
# Pretty printing of ANOVA summary
pg.print_table(aov)

ANOVA SUMMARY
Source SS DF1 DF2 MS F p-unc np2 eps
Group 4.465 1 58 4.465 4.131 0.047 0.066 -
Time 9.359 2 116 4.679 4.940 0.008 0.078 0.998
Interaction 6.539 2 116 3.269 3.452 0.035 0.056 -

We can see that there is indeed a significant interaction, F(2, 116)=3.45, p=.035. The effect size (partial eta-square) of this interaction is .056.

However, this does not tell us which specific contrast is actually significant. For this reason, we need to perform post-hocs tests on the interaction. This can be done very easily using the pairwise_ttests function:

posthocs = pg.pairwise_ttests(dv='Scores', within='Time', between='Group',
                              subject='Subject', data=df)
pg.print_table(posthocs)

which gives us (note that for display purpose I removed some rows and columns from the original table):

POST HOC TESTS
Time A B T-val p-unc Eff_size Eff_type BF10
August Control Meditation 0.733 0.466 0.187 hedges 0.329
January Control Meditation -1.434 0.157 -0.365 hedges 0.619
June Control Meditation -2.744 0.008 -0.699 hedges 5.593

Our visual impression is therefore confirmed: there is a significant increase in test scores in the meditator group 12 months after the beginning of the experiment (T=-2.7, p-unc=.008, Bayes Factor = 5.593). The corrected effect size (Hedges g) is approximately 0.70 and can therefore be considered, according to Cohen's rule of thumb, as large.

Appendix

Correction for multiple comparisons

If you have a large number of groups and/or measurements, you might want to correct the p-values for multiple comparisons. This can be done very easily using the padjust argument of the pairwise_ttests function:

pg.pairwise_ttests(dv='Scores', within='Time', between='Group', subject='Subject',
                   data=df, padjust='holm')

Missing values and unbalanced design

If one subject has one or more missing observations (for example, no tests scores in January), this subject will need to be removed from the ANOVA and post-hocs analyses. This is done automatically by the two aforementionned Pingouin functions. However, if your data really has a lot of missing values, you may want to consider alternative analyses methods, such as linear mixed-effects modelling, which better accomodates for missing data (see the excellent lme4 package in R).

On another note, Pingouin also works well with unbalanced design (i.e. different number of students per group). Please find an example in the full script of this tutorial (link above).

Other ANOVA functions in Pingouin

Further reading